The trigonometry table provides exact values for specific angles in the three primary trigonometric functions: sine (sin), cosine (cos), and tangent (tan).

These values help in solving unknown sides, angles, and areas of triangles efficiently.

Trigonometric Ratios of Standard Angles

Angle (°)	0°	30°	45°	60°	90°

sin θ

0

1/2

√2/2

√3/2

1

cos θ

1

√3/2

√2/2

1/2

0

tan θ

0

1/√3

1

√3

∞

These values are fundamental in trigonometry and are frequently used in calculations involving triangles, physics, and engineering.

Tips and Tricks to Remember the Table of Trigonometry

1. Hand Trick for Sine and Cosine

A quick way to remember sin and cos values for standard angles (0°, 30°, 45°, 60°, 90°) is using your left hand:

Steps:

1. Spread out your left hand and label your fingers from 0° (thumb) to 90° (pinky).
2. To find sin(θ):
   • Count the number of fingers below the one representing your angle.
   • Take the square root of that number and divide by 2.
3. To find cos(θ):
   • Count the number of fingers above the one representing your angle.
   • Take the square root of that number and divide by 2.

Example:

For sin 30°, there is 1 finger below, so:

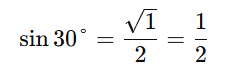
For cos 30°, there are 3 fingers above, so:

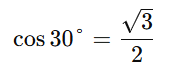
2. Simple Number Pattern for Sine and Cosine

Use the following pattern to remember sine values:

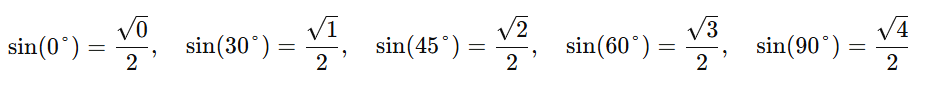
For cosine values, just reverse the sine values!

3. Trick for Tangent Values

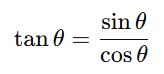
Using this, you get:

• tan 0° = 0
• tan 30° = 1/√3
• tan 45° = 1
• tan 60° = √3
• tan 90° = ∞

A simple trick: tan values increase from 0 to infinity as the angle increases from 0° to 90°.

4. Mnemonic for Sin, Cos, and Tan

A simple phrase to remember sin, cos, and tan ratios:

“Some People Have, Curly Brown Hair, Through Proper Brushing”

• Some People Have → Sine = Perpendicular / Hypotenuse
• Curly Brown Hair → Cosine = Base / Hypotenuse
• Through Proper Brushing → Tangent = Perpendicular / Base

Steps to Create a Trigonometry Table

Creating a trigonometry table involves calculating the values of sine (sin), cosine (cos), and tangent (tan) for standard angles (0°, 30°, 45°, 60°, and 90°). Follow these steps to generate the table:

Step 1: Understand Trigonometric Ratios

The three primary trigonometric functions are:

• sin(θ) = Perpendicular / Hypotenuse
• cos(θ) = Base / Hypotenuse
• tan(θ) = Perpendicular / Base

Since all values are derived from a right-angled triangle, we use the unit circle or special triangles to calculate them.

Step 2: Use Special Triangles

We use two special right-angled triangles to derive exact values:

1. 45°-45°-90° Triangle

• The sides are 1 : 1 : √2 (for 45°)
• Using trigonometric ratios:
  • sin 45° = 1/√2 = √2/2
  • cos 45° = 1/√2 = √2/2
  • tan 45° = 1/1 = 1

2. 30°-60°-90° Triangle

tan 60° = √3

The sides are 1 : √3 : 2 (for 30° and 60°)

Using trigonometric ratios:

sin 30° = 1/2

cos 30° = √3/2

tan 30° = 1/√3

sin 60° = √3/2

cos 60° = 1/2

Step 3: Fill in the Trigonometry Table

Now, organize the values into a table:

Angle (°)	0°	30°	45°	60°	90°
sin θ	0	1/2	√2/2	√3/2	1
cos θ	1	√3/2	√2/2	1/2	0
tan θ	0	1/√3	1	√3	∞

Step 4: Use the Pattern Trick for Sine and Cosine

To easily remember sin values, use this formula:

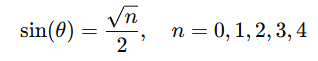
For cosine values, reverse the sine sequence.

Step 5: Calculate Tangent Values

Since tan(θ) = sin(θ) / cos(θ), divide corresponding sine and cosine values to get tangent values.

Step 6: Extend the Table for Reciprocal Functions (Optional)

For a complete table, include:

• Cosecant (csc θ) = 1/sin θ
• Secant (sec θ) = 1/cos θ
• Cotangent (cot θ) = 1/tan θ

Trigonometry Chart

Angle (°)	0°	30°	45°	60°	90°
sin θ	0	1/2	√2/2	√3/2	1
cos θ	1	√3/2	√2/2	1/2	0
tan θ	0	1/√3	1	√3	∞
csc θ	∞	2	√2	2/√3	1
sec θ	1	2/√3	√2	2	∞
cot θ	∞	√3	1	1/√3	0

Key Points:

• sin and cos values follow a pattern:
  • sin θ = √(n)/2, where n increases from 0 to 4 for 0° to 90°.
  • cos θ follows the reverse order of sin θ values.
• tan θ = sin θ / cos θ.
• Reciprocal Functions:
  • csc θ = 1 / sin θ
  • sec θ = 1 / cos θ
  • cot θ = 1 / tan θ

FAQs on Trigonometric Table

1. What is a Trigonometric Table?

A trigonometric table is a chart that provides exact values of sine (sin), cosine (cos), tangent (tan), and other trigonometric ratios for standard angles like 0°, 30°, 45°, 60°, and 90°.

2. Why is the Trigonometry Table Important?

The trigonometry table is essential for solving problems in geometry, physics, engineering, and navigation. It helps in:

• Finding unknown sides and angles in triangles.
• Solving trigonometric equations.
• Calculating distances in astronomy and geography.